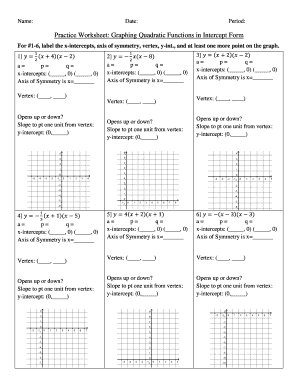
SchoolRack 9.3 Vertex Form Worksheet 2013-2025 free printable template
Show details
Algebra 1-2 Name: 9.3 Vertex Form Worksheet Period: Given that vertex form of a quadratic function is ?????? ? ??? ??? ??? ? ?, graph the parabola and state how it was translated from ?????? ? ? ???
pdfFiller is not affiliated with any government organization
Get, Create, Make and Sign graphing quadratic functions in standard form worksheet 1
Edit your graphing quadratics from standard form worksheet form online
Type text, complete fillable fields, insert images, highlight or blackout data for discretion, add comments, and more.
Add your legally-binding signature
Draw or type your signature, upload a signature image, or capture it with your digital camera.

Share your form instantly
Email, fax, or share your let's graph quadratic equations worksheet answers form via URL. You can also download, print, or export forms to your preferred cloud storage service.
How to edit graphing quadratics by factoring worksheet online
To use our professional PDF editor, follow these steps:
1
Set up an account. If you are a new user, click Start Free Trial and establish a profile.
2
Prepare a file. Use the Add New button. Then upload your file to the system from your device, importing it from internal mail, the cloud, or by adding its URL.
3
Edit graphing quadratic functions in standard form worksheet. Replace text, adding objects, rearranging pages, and more. Then select the Documents tab to combine, divide, lock or unlock the file.
4
Get your file. When you find your file in the docs list, click on its name and choose how you want to save it. To get the PDF, you can save it, send an email with it, or move it to the cloud.
It's easier to work with documents with pdfFiller than you can have believed. Sign up for a free account to view.
Uncompromising security for your PDF editing and eSignature needs
Your private information is safe with pdfFiller. We employ end-to-end encryption, secure cloud storage, and advanced access control to protect your documents and maintain regulatory compliance.
How to fill out graphing quadratics in standard form worksheet
How to fill out SchoolRack 9.3 Vertex Form Worksheet
01
Start by opening the SchoolRack platform and navigating to the Vertex Form Worksheet section.
02
Read through any introductory materials or instructions provided for the worksheet.
03
Identify the specific quadratic functions you will be working with, which should be in vertex form (y = a(x - h)^2 + k).
04
For each quadratic function, note the values of a, h, and k from the function.
05
Fill in the worksheet's fields with the corresponding values of h and k, which represent the vertex (h, k) of the parabola.
06
Use the value of 'a' to determine the direction and width of the parabola; write any necessary notes in the provided sections.
07
If there are graphs to complete, use the vertex coordinates and the direction indicated by 'a' to sketch the graph accurately.
08
Review your responses for accuracy before submitting or saving the worksheet.
Who needs SchoolRack 9.3 Vertex Form Worksheet?
01
Students who are learning about quadratic functions and their properties.
02
Teachers who are providing exercises related to vertex form in algebra courses.
03
Tutors and educators who assist students in understanding the concept of vertex form and parabolas.
Fill
worksheet graphing quadratics from standard form answer key pdf
: Try Risk Free
Our user reviews speak for themselves
Read more or give pdfFiller a try to experience the benefits for yourself
For pdfFiller’s FAQs
Below is a list of the most common customer questions. If you can’t find an answer to your question, please don’t hesitate to reach out to us.
How can I get quadratic functions worksheet with answers pdf?
It's simple with pdfFiller, a full online document management tool. Access our huge online form collection (over 25M fillable forms are accessible) and find the quadratic graphs worksheet with answers in seconds. Open it immediately and begin modifying it with powerful editing options.
How do I edit graphing quadratics worksheets in Chrome?
Install the pdfFiller Google Chrome Extension to edit graphing quadratic functions worksheet and other documents straight from Google search results. When reading documents in Chrome, you may edit them. Create fillable PDFs and update existing PDFs using pdfFiller.
How do I fill out graph quadratic functions in standard form worksheet on an Android device?
Use the pdfFiller app for Android to finish your graphing parabolas in standard form worksheet. The application lets you do all the things you need to do with documents, like add, edit, and remove text, sign, annotate, and more. There is nothing else you need except your smartphone and an internet connection to do this.
What is SchoolRack 9.3 Vertex Form Worksheet?
SchoolRack 9.3 Vertex Form Worksheet is a form used for reporting financial data and calculations related to taxes, specifically in the context of Vertex tax software.
Who is required to file SchoolRack 9.3 Vertex Form Worksheet?
Individuals or businesses who have transactions that require tax reporting through Vertex software are required to file the SchoolRack 9.3 Vertex Form Worksheet.
How to fill out SchoolRack 9.3 Vertex Form Worksheet?
To fill out the SchoolRack 9.3 Vertex Form Worksheet, start by entering your personal or business information, then provide the necessary financial data, and complete any calculations as per the instructions provided in the worksheet.
What is the purpose of SchoolRack 9.3 Vertex Form Worksheet?
The purpose of the SchoolRack 9.3 Vertex Form Worksheet is to collect and organize information needed for accurate tax reporting and to ensure compliance with tax regulations.
What information must be reported on SchoolRack 9.3 Vertex Form Worksheet?
The information that must be reported includes income details, deductible expenses, and any other relevant financial data that pertains to the taxpayer's obligations.
Fill out your SchoolRack 93 Vertex Form Worksheet online with pdfFiller!
pdfFiller is an end-to-end solution for managing, creating, and editing documents and forms in the cloud. Save time and hassle by preparing your tax forms online.

Quadratic Functions In Standard Form Worksheet is not the form you're looking for?Search for another form here.
Keywords relevant to graphing quadratics in standard form worksheet answers
Related to answer key graphing quadratic functions worksheet answers algebra 2
If you believe that this page should be taken down, please follow our DMCA take down process
here
.