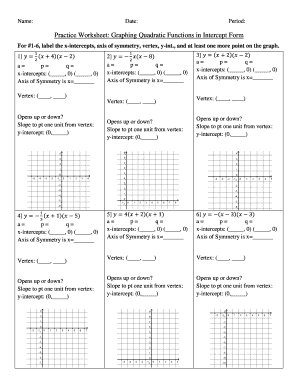
SchoolRack 9.3 Vertex Form Worksheet 2013-2025 free printable template

Comprehensive Guide to Vertex Form of Quadratic Functions

What is vertex form?

Vertex form is a specific way of expressing a quadratic function. This format is represented by the equation y = a(x-h)² + k, where (h, k) is the vertex of the parabola. The vertex form allows for easy identification of the parabola's maximum or minimum point, making it invaluable for graphing and transformations.

1. A quadratic function expressed as y = a(x-h)² + k, showing its vertex clearly.
2. In this formula, 'a' indicates the direction and width of the parabola, while 'h' and 'k' denote the vertex coordinates.
3. Unlike the standard form y = ax² + bx + c, vertex form directly reveals the vertex, facilitating graphing and transformations.

How do you graph using vertex form?

Graphing a parabola in vertex form is a systematic approach that brings clarity to the process. By following straightforward steps, you can effectively represent the quadratic function visually.

1. Start by locating the vertex (h, k) in the equation to determine the parabola's maximum or minimum point.
2. The axis of symmetry is the vertical line x = h, which divides the parabola into two mirror-image halves.
3. Generate points by substituting x-values into the vertex form equation to find corresponding y-values, allowing you to sketch the parabola accurately.
4. Consider graphing y = 2(x-3)² + 1. The vertex (3, 1) indicates the highest point, while plotting additional points around this central point provides a complete graph.

What does translation of a parabola mean?

Translation refers to shifting the entire graph of a function from its original position without changing its shape. In vertex form, translations occur by varying the values of h and k in the equation.

1. When h and k are altered, the vertex moves, resulting in a horizontal and/or vertical shift of the parabola.
2. For the equation y = 2(x-5)² + 3, the vertex shifts to (5, 3) from the origin, translating the graph right and up.
3. Transformations include shifts (horizontal and vertical), stretches (how wide or narrow the parabola appears), and reflections (which direction the parabola opens).

How can you practice with worksheets?

Worksheets are an effective way to consolidate understanding of vertex form and its applications. Using tools like pdfFiller allows for interactive engagement with the material.

1. Fill out the provided quadratic functions in the worksheet. This exercise will enhance your grasp of the concepts.
2. Engage with practice questions that focus on identifying vertices and performing translations using vertex form.
3. Utilize sample vertex form equations provided in the worksheet to apply what you’ve learned through hands-on practice.

How does pdfFiller help in document creation?

pdfFiller provides users with powerful tools to create, edit, and manage worksheets online. This user-friendly platform simplifies the process of document management in educational contexts.

1. With pdfFiller, users can easily author and refine their own quadratic function worksheets, ensuring they meet educational needs.
2. The platform offers interactive features that enhance collaboration and engagement, making learning more effective.
3. pdfFiller provides straightforward guidance to upload, edit, sign, and share documents, creating a seamless user experience.

What are the advantages of managing math worksheets online?

The benefits of cloud-based document management tools like pdfFiller include improved accessibility, collaboration, and organization of academic materials.

1. Users can access their math worksheets anytime and anywhere, fostering continuous learning.
2. Share your documents with peers for collaborative problem-solving and studying, enhancing comprehension of vertex form.
3. Using cloud management increases efficiency in document handling, making it easier to focus on learning.

What are the key takeaways on vertex form?

Understanding vertex form is crucial for mastering quadratic equations and their graphing. Regular practice is essential to build confidence in transformations and vertex identification.

1. Remember the importance of the vertex and the way changes in h and k affect the graph.
2. Consistent practice using tools like pdfFiller enables mastery of these concepts and boosts your proficiency.
3. Make full use of platforms like pdfFiller for interactive learning and ensure academic success in mathematics.

Frequently Asked Questions about vertex form to standard form worksheet

What is vertex form used for?

Vertex form is primarily used to easily graph quadratic functions and identify their key features such as the vertex and axis of symmetry. It's also instrumental in understanding how changes to the equation affect the graph.

How do you identify the vertex in vertex form?

In the vertex form equation y = a(x-h)² + k, the vertex is the point (h, k). You can directly read these values off the equation since they are the coordinates at which the parabola reaches its maximum or minimum.

What advantages does pdfFiller offer for math worksheets?

pdfFiller allows users to create, edit, and manage math worksheets efficiently. Its interactive features facilitate collaboration, making it a valuable tool for teachers and students alike.

Can you explain translation in vertex form?

Translation in vertex form occurs when the values of h and k are altered, shifting the graph horizontally or vertically without changing its shape. This helps students visualize how quadratic functions move on a coordinate plane.

How can I practice vertex form equations?

You can practice vertex form equations by completing worksheets specifically designed for this purpose. pdfFiller provides a platform where you can find and fill out these worksheets interactively, enhancing your learning experience.